1171. Remove Zero Sum Consecutive Nodes from Linked List

Today is a medium problem.
We need to remove the zero-sum parts of the linked list.
I can't resolve it by myself, so just refer to the solutions.
Even if it's not that clear after reading the answer.
The example linked list is [1, 2, -3, 3, 1].
-
Create a dummy node to create a new linked list.
Because the head might be the one of the zero-sum parts.
Initialize
prefix_sumto record node sum andprefix_sum_to_nodeto record prefix sum and node. -
First traversal:
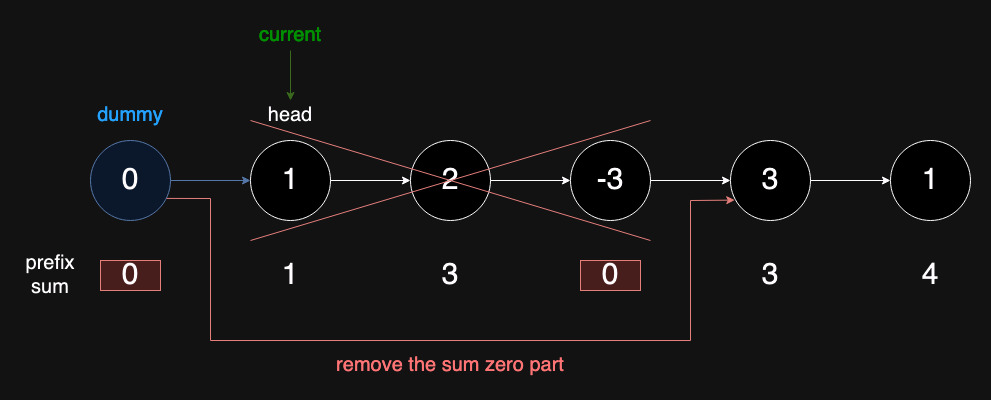
Calculate the prefix sum for each node.
Record the node with the prefix sum.
The node will be overridden with the same prefix sum.
This helps us to remove the zero-sum part in the next step.
- The
prefix_sum_to_nodewill look like this:
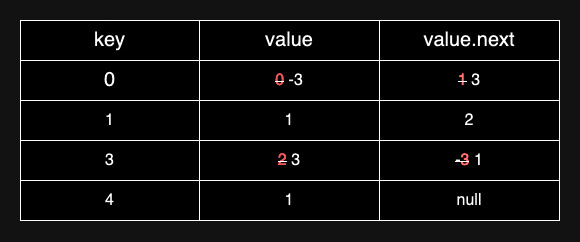
- The
-
Second traversal:
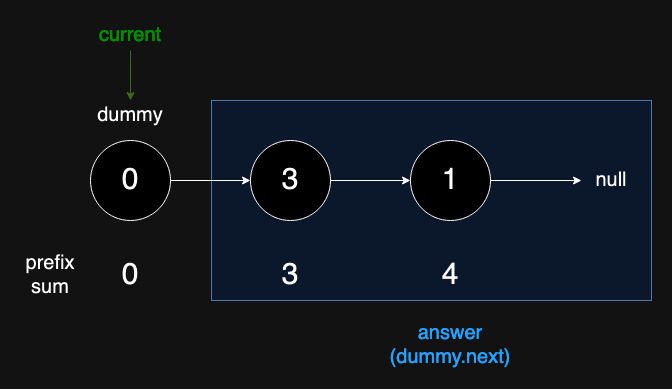
Calculate the prefix sum again but use the values in
prefix_sum_to_node.Linked with the
prefix_sum_to_nodewill generate the answer linked link.Don't forget to remove the first dummy part.
from typing import Optional # Definition for singly-linked list. class ListNode: def __init__(self, val=0, next=None): self.val = val self.next = next class Solution: def removeZeroSumSublists( self, head: Optional[ListNode], ) -> Optional[ListNode]: dummy = ListNode(0, head) prefix_sum = 0 prefix_sum_to_node = {0: dummy} current = head while current: prefix_sum += current.val prefix_sum_to_node[prefix_sum] = current current = current.next prefix_sum = 0 current = dummy while current: prefix_sum += current.val current.next = prefix_sum_to_node[prefix_sum].next current = current.next return dummy.next
Time complexity: O(n)
Traversing the linked list twice takes O(2n).
We can simply this to O(n).
Space complexity: O(n)
We use an additional hash table, prefix_sum_to_node.
It will takes O(n) in the worst-case scenario, where all the prefix sums are different.
The length will be the same as the linked list.