57. Insert Interval

Overview

Question Link

Insert the new interval into intervals array.

If the new intervals crosses several intervals, they should combine into one interval.

Solution 1: Linear Search

Algorithm

1. Initialize n as the length of intervals.
   i will point to index we're current handling, defaulting to 0.
   Initialize a new list answer to save the interval results.
   Destructure new_interval into new_start and new_end for increased readable.

2. Check if current interval end is smaller than new_start.
   It means the current interval is entirely before the new internal.
   Append the current interval to the answer.

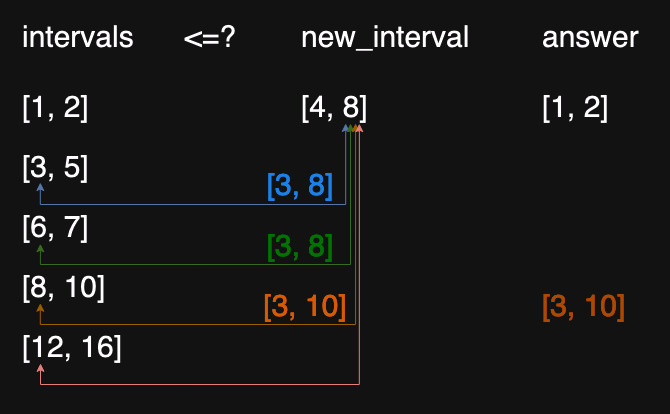
3. Check if new_end is greater than or equals to current interval start
   It means the new interval should combine with the current interval.
   Append the new interval to the answer after all combining is finished.

4. Check if there still some intervals not appended to the answer. Append the remaining intervals to the answer.

Implement

class Solution:
    def insert(
        self,
        intervals: list[list[int]],
        new_interval: list[int],
    ) -> list[list[int]]:
        n = len(intervals)
        i = 0
        answer: list[list[int]] = []
        new_start, new_end = new_interval

        while i < n and intervals[i][1] < new_start:
            answer.append(intervals[i])
            i += 1

        while i < n and new_end >= intervals[i][0]:
            new_start = min(new_start, intervals[i][0])
            new_end = max(new_end, intervals[i][1])
            i += 1
        answer.append([new_start, new_end])

        while i < n:
            answer.append(intervals[i])
            i += 1

        return answer

Complexity Analysis

Time complexity: O(n)

The variable i will increase from 0 to n.

We only iterate through the intervals once.

Space complexity: O(1)

We only use an additional list for saving the answer.